Simplify your tasks, supercharge your workflow, and thrive in your independent journey





Why Heyweek?
Experience the power of having all your freelancing tools in one intuitive platform
Simplify your day-to-day
Say goodbye to juggling multiple tools and hello to an efficient workflow
Boost your freelance success
Tools designed to give you control and clarity
Effortlessly create and manage invoices with a touch of automation. Our user-friendly invoicing system is designed to save time and reduce errors
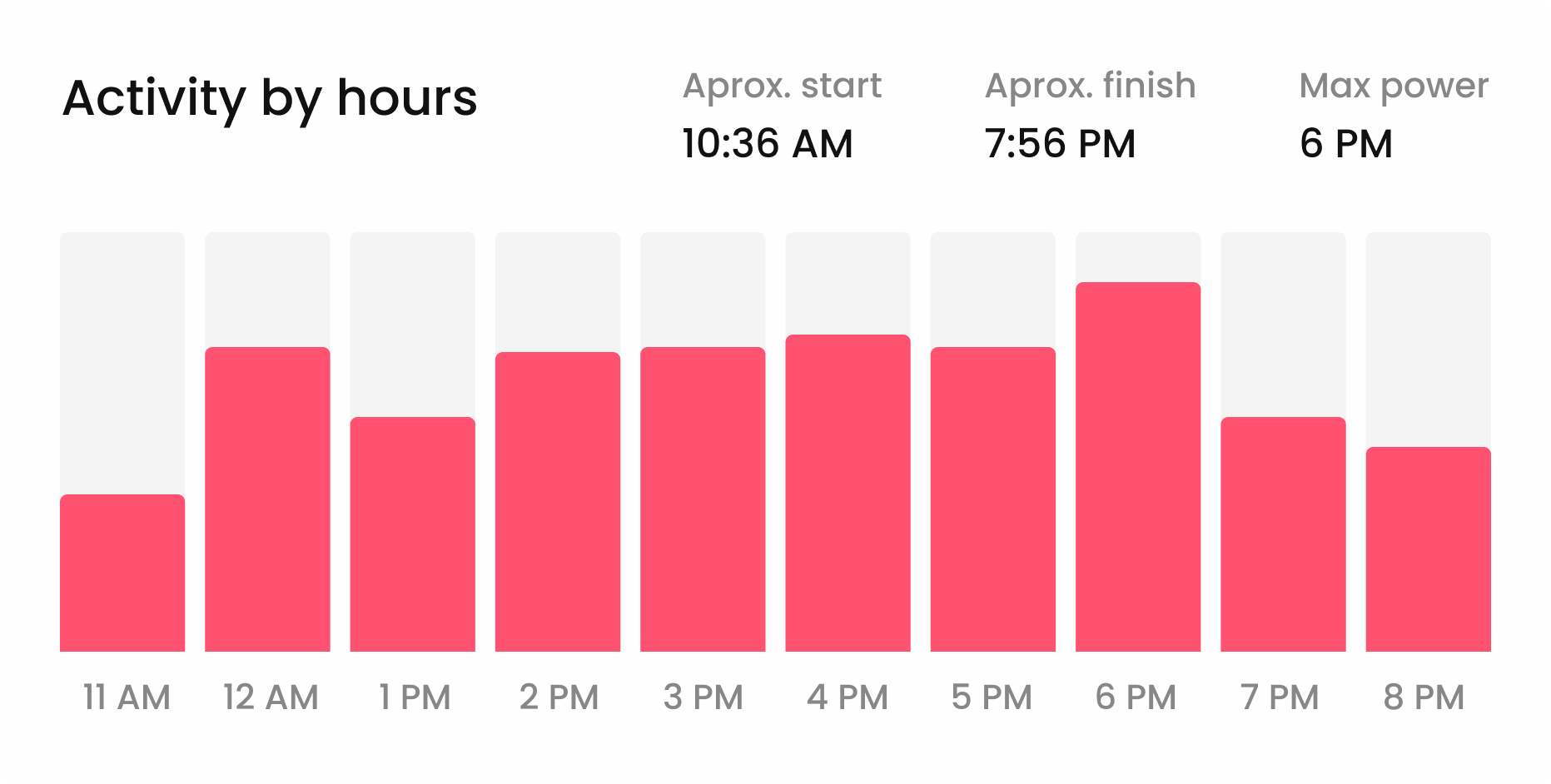
Maximize your billable hours with intuitive time tracking. Understand where your time goes and optimize your efforts for better profitability
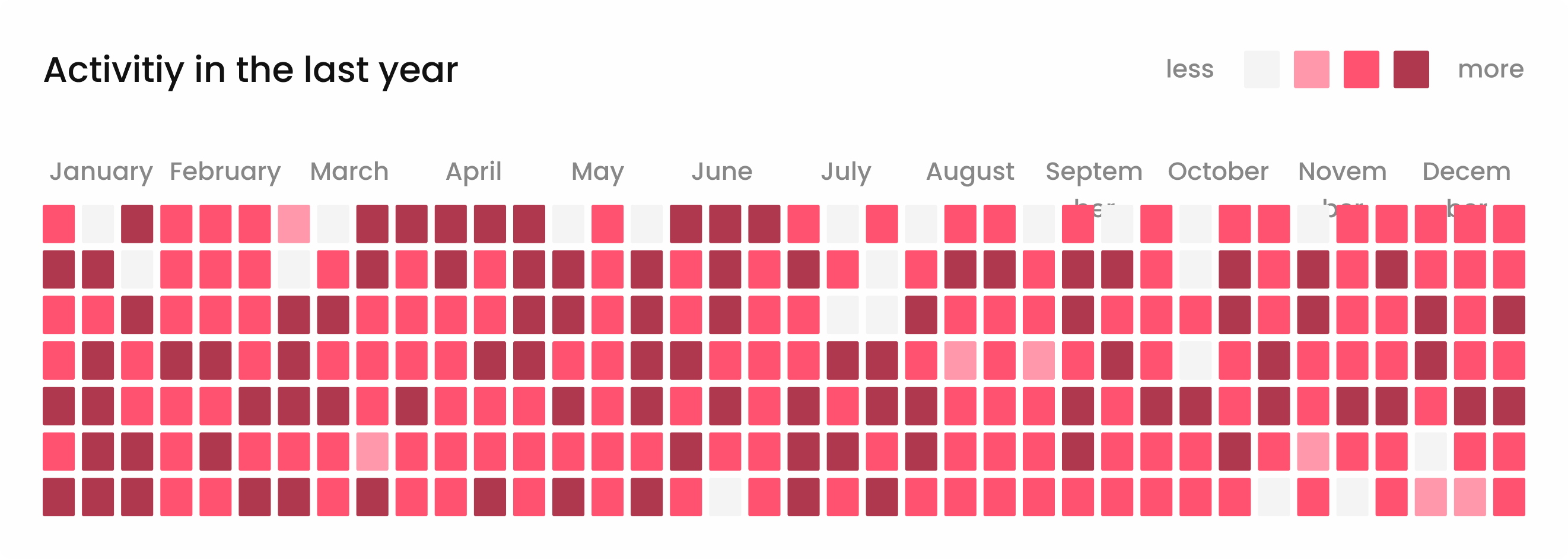
Keep a keen eye on your financial health. Track incoming and outgoing funds, ensuring you always have a clear picture of your business's financial status
Offer your clients a seamless experience. Provide them with a dedicated space to view projects, share feedback, and collaborate without the back-and-forth
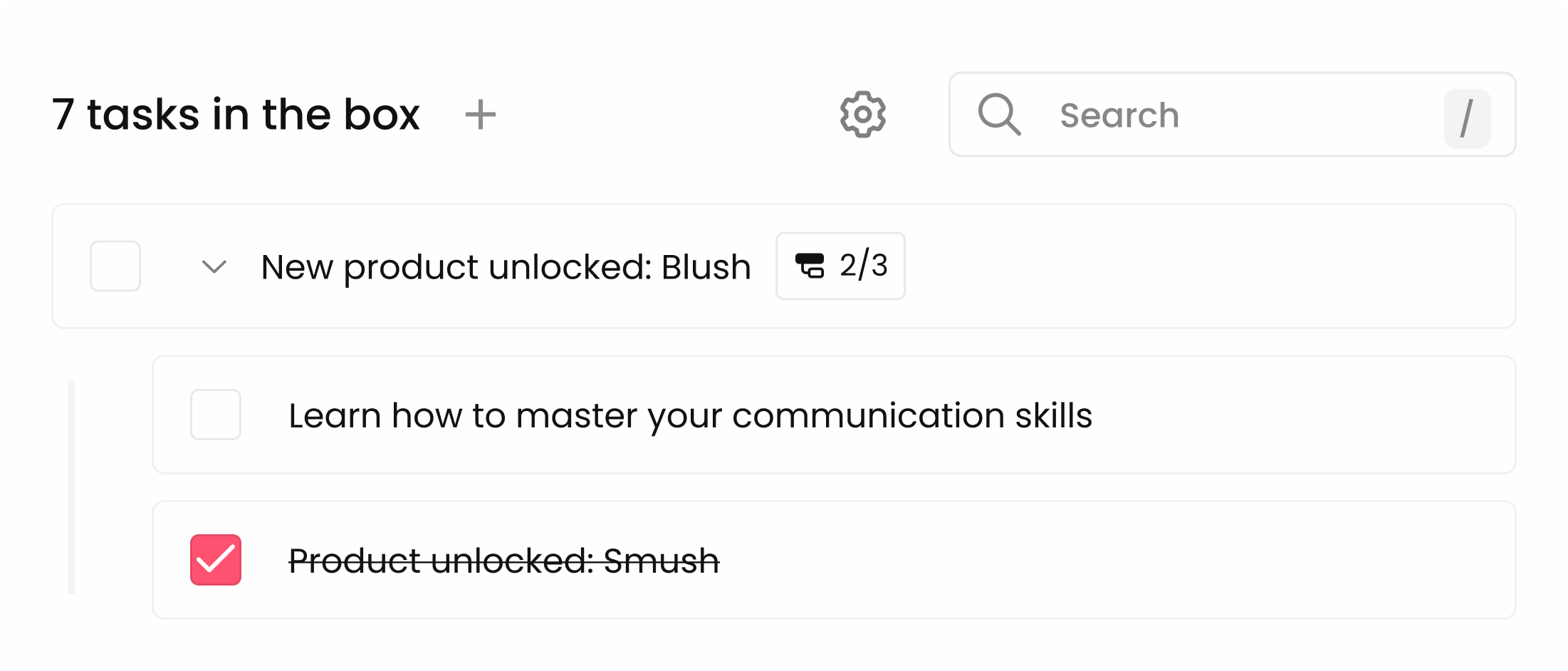
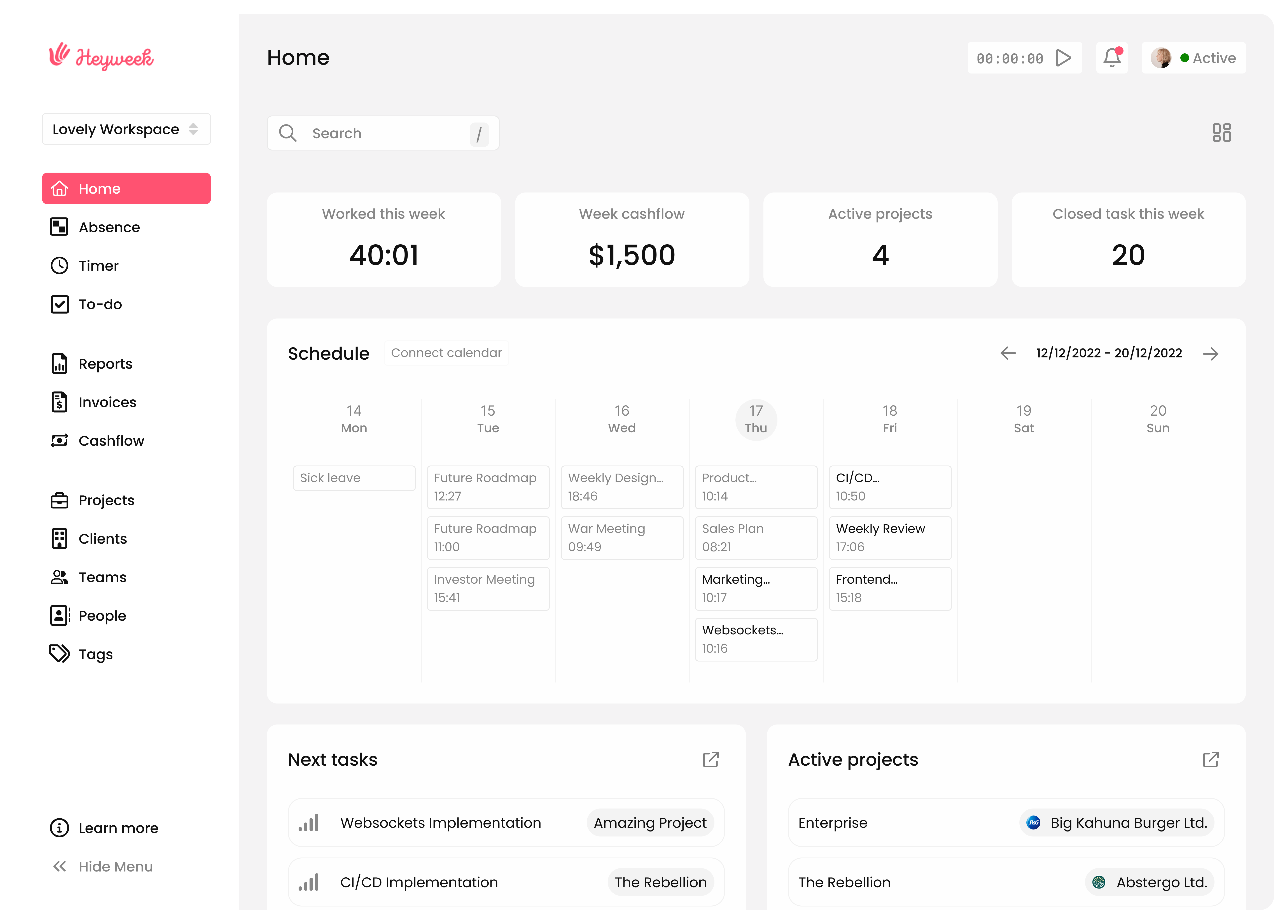
Bring every element of your work together in one place. With integrated time tracking, task management, and invoicing
With Heyweek, there's always more. Dive into a suite of additional tools designed to support every aspect of your freelance journey, making every task a breeze
Usecases
Discover how freelancers like you make the most of their day, seamlessly blending Heyweek into their daily routines and projects.
Ensure you always take advantage of every billable minute and have a clear work record.
Create, send, and manage all your invoices, saving time and reducing errors.
Keep all your client information, communication, and project details in one place.
Monitor income, track expenses, and easily stay on top of your financial health.
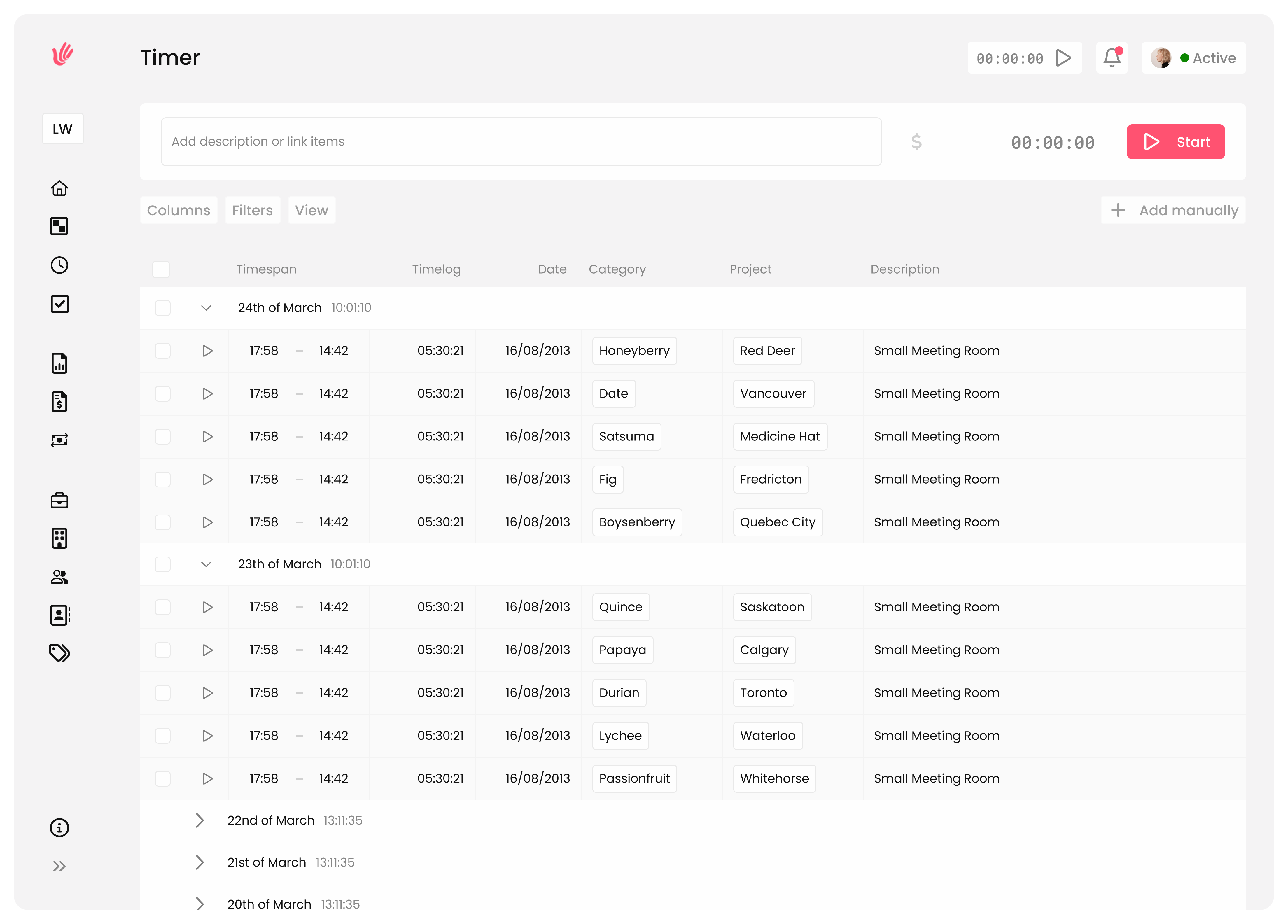
Track every second, bill every penny
Take control of your time and ensure that every minute of your work is accurately logged and accounted for. Start, pause, and log time with a clear workday view.
Quickly start and stop timers as you switch between tasks.
Generate detailed time reports to analyze your productivity patterns.
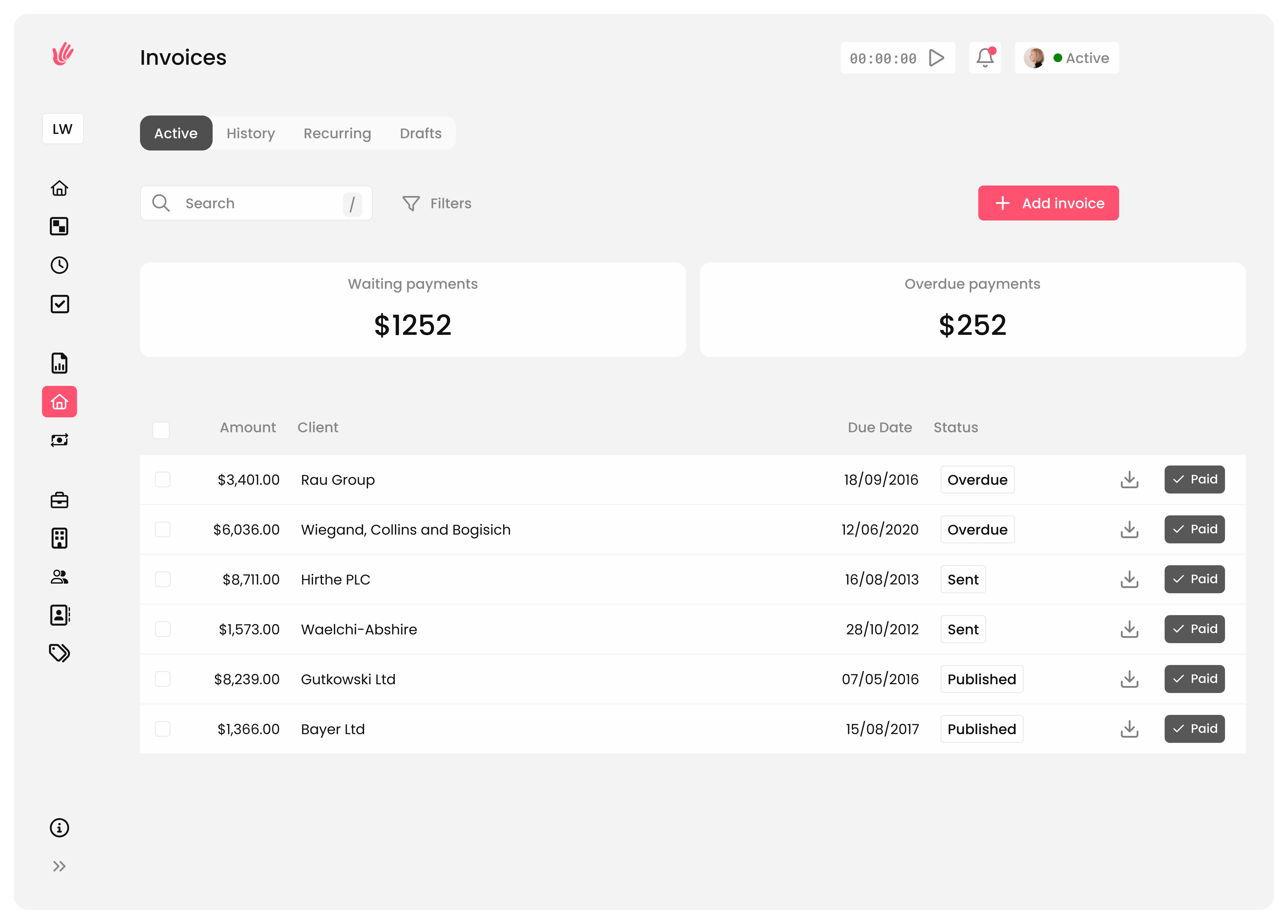
Fast, accurate, and hassle-free invoicing
Create professional invoices in moments, send them directly to your clients, and keep track of payments all in one place.
Create and send professional invoices.
Track payments and receive alerts.
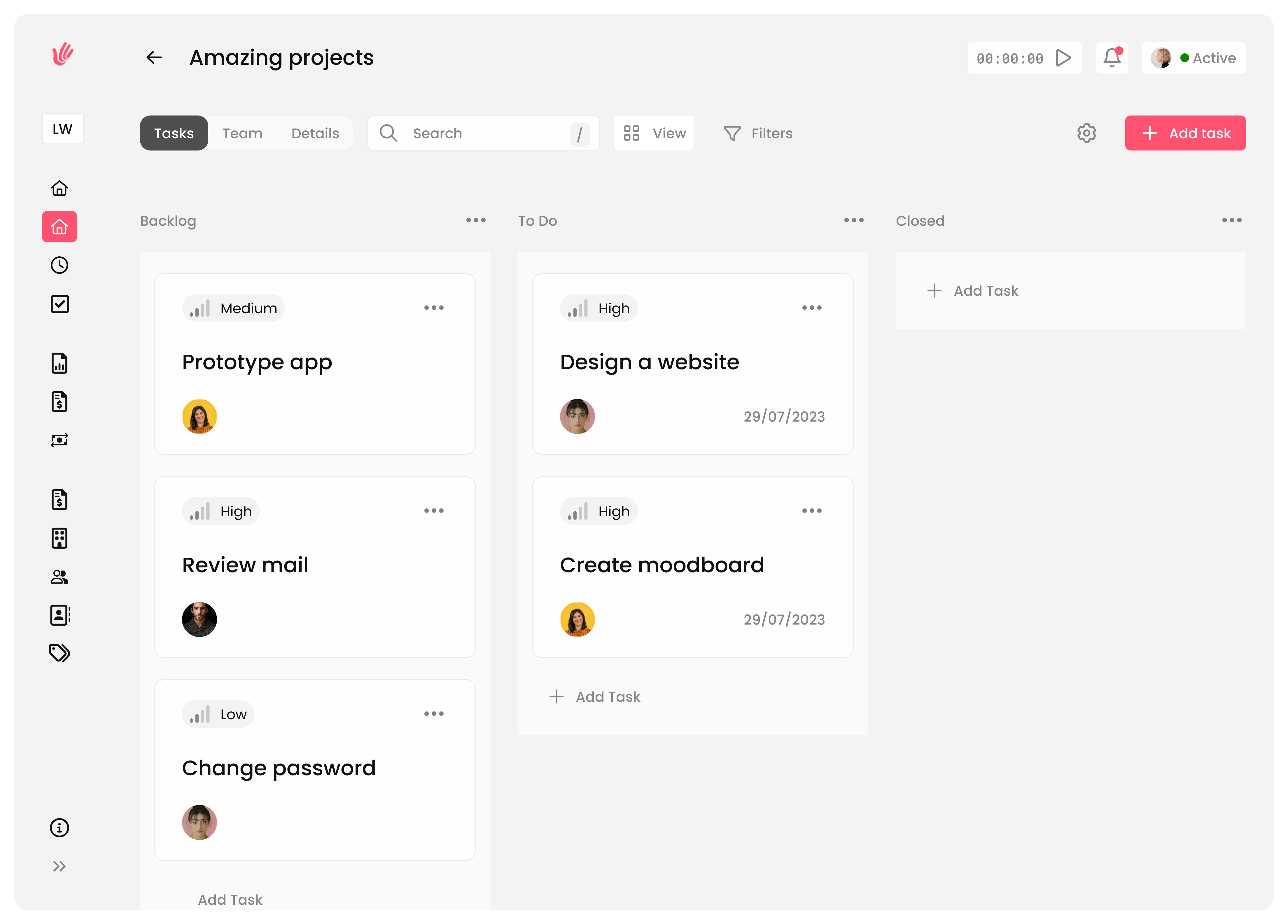
Organize, prioritize, and deliver
Manage deadlines, set priorities, and stay ahead of your schedule, ensuring every project succeeds.
Integrate time tracking, tasks, and invoices within projects.
Easily set priorities and deadlines.
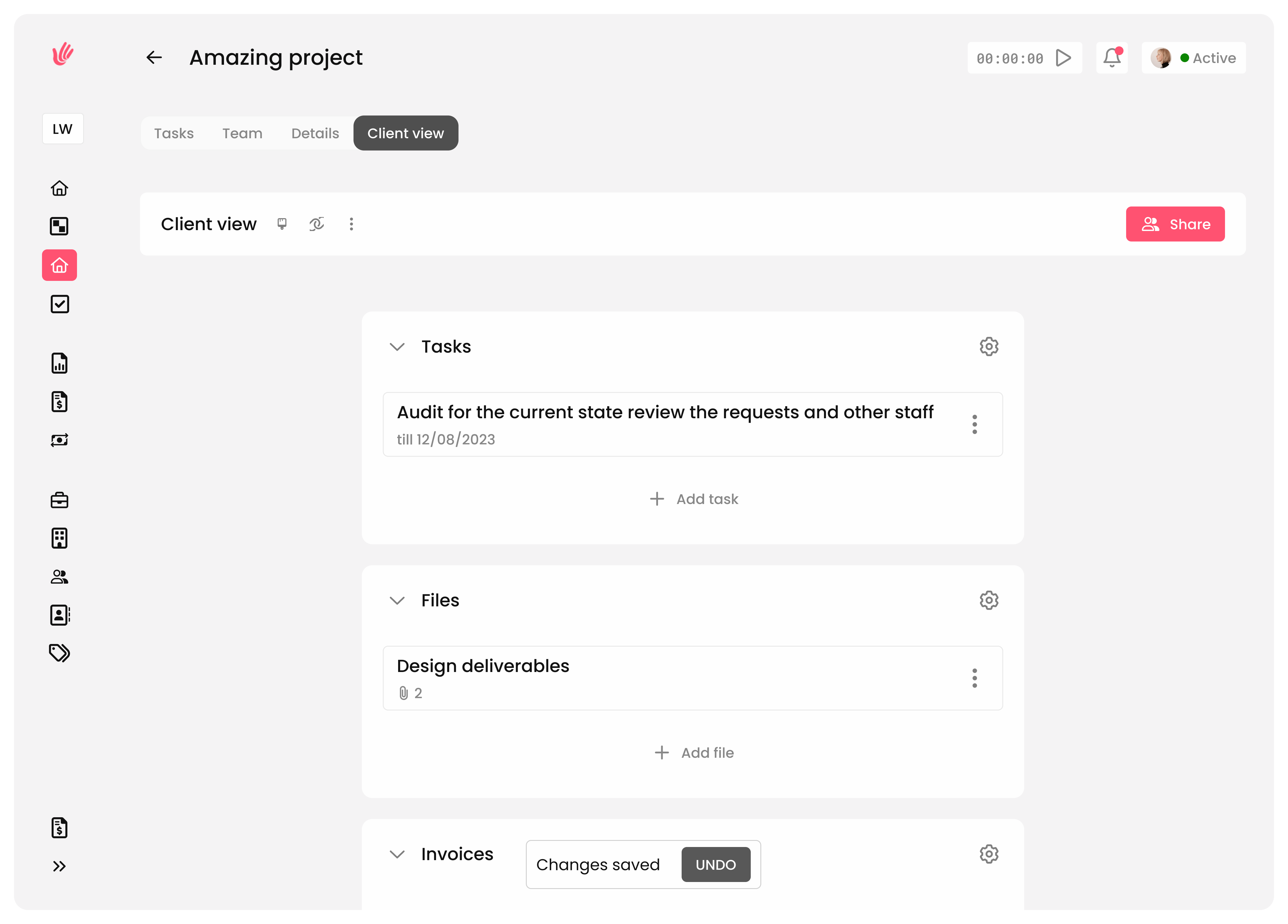
All your client information, one click away
Organize all crucial client information and keep it easily accessible to ensure you're always prepared for every meeting and correspondence.
Centralize client information, notes, and communication history.
Improve response times and client satisfaction.
Empowering your Heyweek journey with instant responses to popular inquiries.

Heyweek uniquely designs a comprehensive toolbox to provide freelancers with everything they need in one place, including invoice management, time tracking, client portals, and project organization.

Getting started with Heyweek is a breeze! You can set up your account and utilize the tools in just a few minutes.

Heyweek is globally accessible and supports multiple languages to cater to our diverse user base. We offer support in English, Swedish, Japanese, French, Spanish, German.

Yes, you can access Heyweek from various devices. While the core app is web-based and optimized for desktop use, a mobile app is also being developed to provide even greater flexibility for freelancers.
Free for 14 days - No credit card required